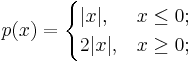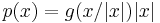Asymmetric norm

In mathematics, an asymmetric norm on a vector space is a generalization of the concept of a norm.

Definition

Let X be a real vector space. Then an asymmetric norm on X is a function p : X → R satisfying the following properties:

• non-negativity: for all x ∈ X, p(x) ≥ 0;
• definiteness: for x ∈ X, x = 0 if and only if p(x) = p(−x) = 0;
• homogeneity: for all x ∈ X and all λ ≥ 0, p(λx) = λp(x);
• the triangle inequality: for all x, y ∈ X, p(x + y) ≤ p(x) + p(y).

Examples

• On the real line R, the function p given by

is an asymmetric norm but not a norm.

• More generally, given a strictly positive function g : Sⁿ⁻¹ → R defined on the unit sphere Sⁿ⁻¹ in Rⁿ (with respect to the usual Euclidean norm |·|, say), the function p given by

is an asymmetric norm on Rⁿ but not necessarily a norm.

References

• Cobzaş, S. (2006). "Compact operators on spaces with asymmetric norm". Stud. Univ. Babeş-Bolyai Math. 51 (4): 69–87. ISSN 0252-1938. MR2314639.